Future Value Calculation and the Rule of 72

Getting down and dirty with the Compound Annual Growth Rate (CAGR) formula

The Basics

Let’s say you have an asset worth $100 now, and you want to find out what it’s value will be in 5 years if it grows at a rate of 10% per annum and interest is compounded.

The equation is simple. The asset’s future value (FV) and present value (PV) are related as follows:
$$FV = PV\times(1+i)^n$$

where i is the rate of interest and n is the number of periods. In our example:

$$FV = $100\times(1+0.10)^5 = $161.051$$

Here the total growth over the 5 years FV/PV is 161.051/100 = 1.61051 . This gives us the total cumulative return r.

$${FV \over PV} = (1+i)^n = 1+r$$

Or expressed in percentage terms:

$$r = [(1+i)^n - 1] \times 100$$

(equation A).

In our example, (1.61051-1) x 100 = 61.051%.

If we rewrite the future value calculation to solve for i:

$$i = \left[FV \over PV\right] ^{1/n} - 1$$

(equation B),

then substituting in for r and in percentage terms:
$$i = [ (1+r)^{1/n} - 1 ] \times 100$$

(equation C).

Note that equations marked A and C are quite symmetrical. The form of Equation B is termed the compound annual growth rate (CAGR).

If we wanted to solve for n, the formula becomes more involved:
$$n = {log(FV) - log(PV) \over log(1+i)}$$

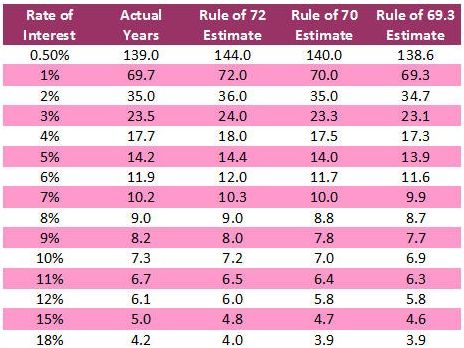
Typically we can use the “Rule of 72” to derive a quick approximation for how long it will take to double an investment value.

---

The Rule of 72

The Rule of 72 is a very simple way of illustrating the growth potential of compound interest. The rule says simply this:
$${72 \over i} \approx n$$
where i is the interest rate in percentage, and n is the number of time periods needed to double the principal.

For example, say an investment fund grows at 12% average annual rate. According to the rule of 72, if money were invested in this fund, then it would double every 6 years (72/12 = 6).

However, the above Rule of 72 merely gives an approximation of the time needed to retain an investment before it doubles in value. The accurate calculation is as follows:
$$n = {ln2 \over ln(1+i)}$$

Alternatively, the Rule of 70, or 69.3 is used for more accuracy at lower interest rates.

Table: Time needed for an investment to double, at different interest rates.